Hierachical Finite State Machines

In this post I talk about hierarchical state machines and present a simple implementation, based on the state pattern. It is by no means a comprehensive explanation, and I skim over some important details (in which we all knows the devil cozily dwells). So if you want to know more you can read the book by Miro Samek, “Practical UML Statecharts in C/C++: Event-Driven Programming for Embedded Systems”, to which this post is (heavily) inspired. The book is a must read for everyone who wants to implement an efficient framework for an event driven, reactive system.

A brief review of classic Finite State Machines

Finite State Machines (FSM for short) are a powerful approach to reducing complexity in code: a system is partitioned in (finite) chunks of behaviors, called states, and during its lifetime the system is always in one (and only one) of these states.  The system receives events, and all the events are handled based on the current state. A state captures the history of the system up to that point, and provides a clear execution context for handling the event, instead of relying on a multitude of (often overlapping) variable and flags and conditional statements. A system can move from one state to another depending on which event occurs by means of state transistions. 

Some state machines use additional variable to represent the state, called extended state variables. In these implementations the state variable represents the qualitative state, while the extended state variables represent the quantitative state. These state machines are often called extended state machines (or state machines with memory). The extended state variables are evaluated in guard conditions during transitions.

Traditional finite state machines are a pretty handy tool but suffers from what is called state explosion: many events are often handled in the same way in multiple states as there’s no way to factor out common behavior in a classical FSM and many transitions and actions are repeated in different states. What is needed is a way to reuse the common behavior in order to share it among different states.

HFSM basic concepts:

Hierachical State Machines address the shortcomings of traditional Finite State Machines. They provide an efficient way of capturing the commonality of behavior between states and can represent the complexity of a sistem avoiding the state explosion. This behavioral ineritance is implemented by using composite states, states that contain other states, and leaf states (which do not). A state diagram becomes a tree, with a top state at the root.

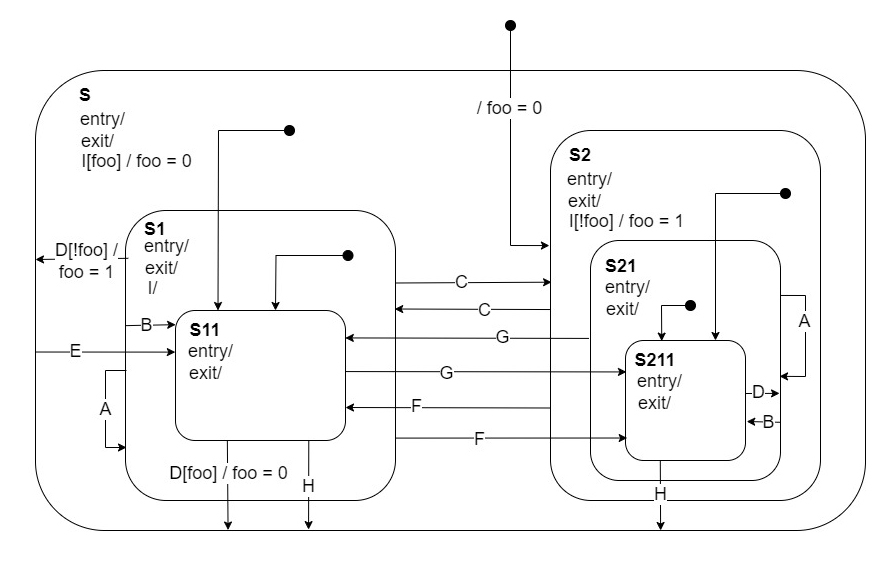
States and state configurations

In every moment the hierarchical state machine is in one defined state, the current state which is always a leaf state. When the state machine is in a specific state, at the same time it’s considered to be in all the enclosing superstates of that state: the actual state is represented by the specific state the HFSM is in, and all the enclosing (composite) superstates of that state. All these states together represent the current state configuration of the HFSM. For this reason, an HFSM is said to be in a current state configuration rather than in specific state:

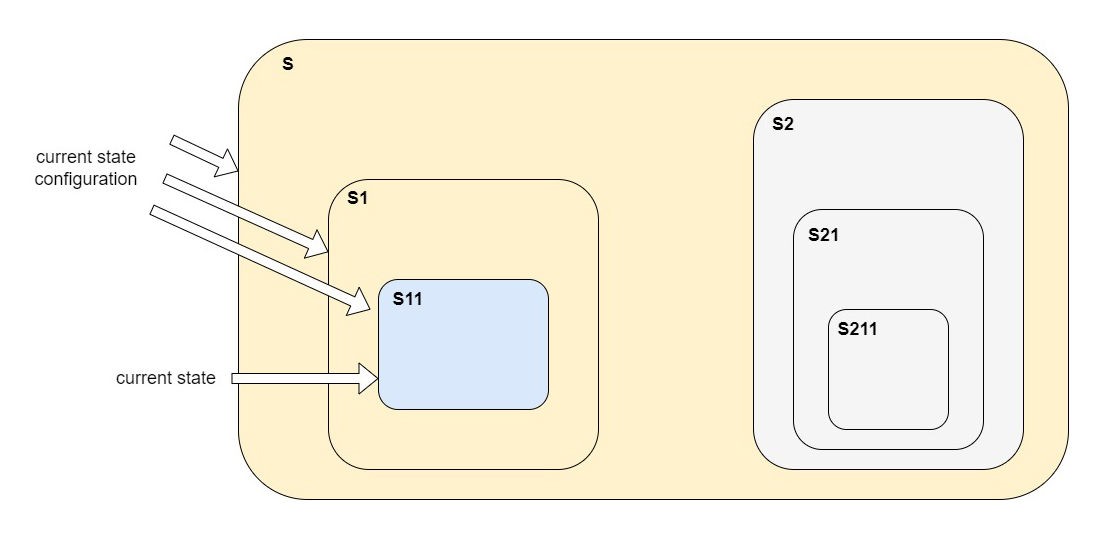
When the state machine receives an event, the current state gets a chance to handle it. If it doesn’t handle it, the event is passed to the current state’s superstate, and so on, until a state handles the event or (if the top state is reached) it is silently discarded.

Transitions

As in traditional FSMs, transistions connect two states, a source state and a target state. In a HFSM the state which is the source of the transition isn’t necessarily the current state but may be a superstate of the current state, and it’s called the main source state; the state which is the target of the transition is called the main target state. Transistioning from a main source state to a main target state means exiting the current states and all the parent states of the current state up to the lowest superstate that is common to both the main source state and the main target state; this state is called the Least Common Ancestor (LCA) of the main source and target states. Note that the LCA itself is not exited. The HFSM then enters the states below the LCA up until the main target state. If the target state is a composite state, the HFMS then enters the substates using initial transitions until it reaches a leaf state:

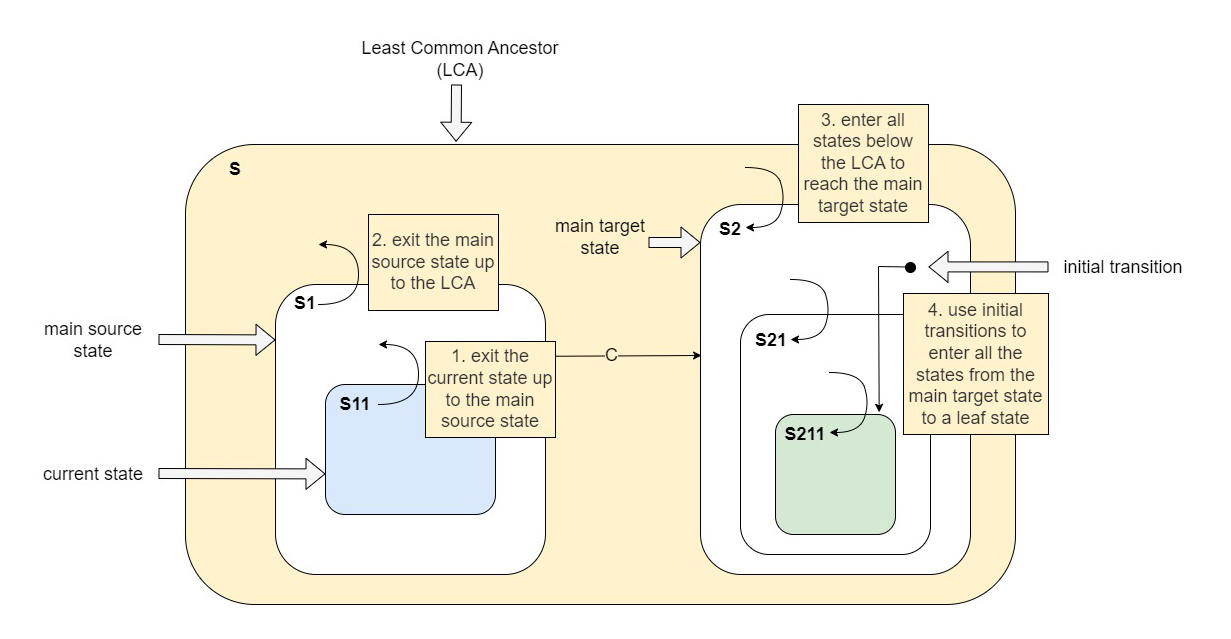
Transitions are indicated with an arrow and the associated event. They can have actions associated with them. In the diagram actions are indicated on the corresponding transition after the /. Transitions can also have guard conditions, indicated in square brackets: guard conditiona often operate on the extended state variables and indicates that the associated transition is taken only if the guard evaluates to true.

HSM Implementation

A HSM can be implemented in several ways. This implementation is focused on simplicity rather than speed performance. It is a variation of the State pattern where the state is an object derived from the state base abstract class: entry and exit actions and initial transitions are implemented as separate methods OnEntry(), OnExit() and OnInitial() respectively, and the generic event handler, OnEvent(), uses a switch statement to discriminate the event to handle:

enum class Signal : uint8_t
{
    A, B, C, D, E, F, G, H, I
};

struct Event
{
    Signal sig;
};

enum class Ret : uint8_t
{
    IGNORED, HANDLED, TRANSITION 
};

class State
{
public:
    virtual ~State() = default;

    virtual void OnEntry(HSM *context) const {}
    virtual void OnExit(HSM *context) const {}
    virtual Ret OnEvent(HSM *context, const Event *event) const = 0;

    bool OnInitial(HSM *context) const
    {
        if (mInitial)
        {
            context->ChangeState(mInitial);
            return true;
        }

        return false;
    }

    void SetParent(State *parent) { mParent = parent; }
    State *GetParent() const { return mParent; }

    void SetInitial(State *initial) { mInitial = initial; }

protected:
    State(const std::string &name) : mName(name), mParent(nullptr), mInitial(nullptr) {}

private:
    std::string mName;
    State *mParent;
    State *mInitial;
};

The OnEntry() method returns a particular value from a Ret enumeration, based on how it handled the event. An Event class is also defined, which contains a value from a Signal enumeration which is only forward declared (it’s definition is provided in the actual state machine implamentation file). A state object mantains a pointer to the parent superstate as well as a pointer to the target state of the target of its initial transition (if the state is a leaf state the pointer is null). A particular state, called the Top state, is defined to act as the root of all other states:

class TopState : public State
{
public:
    Ret OnEvent(HSM *context, const Event *event) const override
    {
        return Ret::IGNORED;
    }
};

Its only task is to implement the event handling method which ignores all events, and to be at the top of the hierarchy of all other states.

The HSM class implements the state machine

class HSM
{
friend class Initial;
friend class S;
friend class S1;
friend class S11;
friend class S2;
friend class S21;
friend class S211;

public:
    void Init(const Event *event = nullptr);
    void Dispatch(const Event *event);
    void ChangeState(State *mainTargetState) { mCurrentState = mainTargetState; }

protected:
    HSM(State *initial) : mCurrentState(initial) {}

    static class TopState sTopState;
private:
    State *mCurrentState;   // state variable

    int mFoo;               // extended state variable
    
    static class TopState sTopState;   // top pseudo state

    static class Initial initial;      // HSM states
    static class S s;
    static class S1 s1;
    static class S11 s11;
    static class S2 s2;
    static class S21 s21;
    static class S211 s211;
};

The base event processor class contains the pointer to the current state and has three member functions:

• a Init() function which dispatches the initial event to the top state, triggering the initial transition from the top state. The passed event can be used to initialize the extended state variables:

void HSM::Init(const Event *event)
{
    Ret ret = mCurrentState->OnEvent(this, event);

    State *initialSourceState = &sTopState;  // top state is the root of all states
    
    do
    {
        std::vector<State*> path;

        // get the path from the target of initial transition to the source of initial transition
        State *state = mCurrentState;
        while (state != initialSourceState)
        {
            path.push_back(state);
            state = state->GetParent();
        }

        // enter all the states from the source of initial transition to the target of initial transition
        for (std::vector<State*>::reverse_iterator rit = path.rbegin(); rit != path.rend(); ++rit)
            (*rit)->OnEntry(this);

        initialSourceState = mCurrentState;    // the source of the new initial transition is the current state
    } while (mCurrentState->OnInitial(this));  // trigger the new initila transition. if leaf state exit loop
}

• a Dispatch() function, the core of the event processor, which dispatches events to the state machine, and is in charge of handling transitions between states: a state only set the main target state of a transition, and the Dispatch() method performs all the necessary work to transition from one state configuration to another:

void HSM::Dispatch(const Event *event)
{
    State *oldState = mCurrentState;

    // find the state that handles the event
    State *state = mCurrentState;
    Ret ret;
    while (state && (ret = state->OnEvent(this, event)) == Ret::IGNORED)
        state = state->GetParent();

    if (state && ret == Ret::TRANSITION)  // event triggered transition
    {
        State *mainSource = state;                
        State *mainTarget = mCurrentState;

        // exit all states up until the main source state
        state = oldState;
        while (state != mainSource)
        {
            state->OnExit(this);
            state = state->GetParent();
        }

        // find the Least Common Ancestor (LCA), the lowest state in the hierarchy which is superstate of both main source and main target states
        // (if the main source state or the main target state are superstate of each other the superstate is the LCA)
        State *LCA = nullptr;
        if (mainSource == mainTarget)         // corner case: self transition
            LCA = mainSource->GetParent();
        else
        {
            State *sourceState = mainSource;
            while (sourceState)
            {
                State *targetState = mainTarget;
                while (targetState && targetState != sourceState)
                    targetState = targetState->GetParent();

                if (targetState)
                {
                    LCA = targetState;
                    break;
                }

                sourceState = sourceState->GetParent();
            }
        }

        // if (!LCA)
        //     ; error

        // exit all states from the main source state up until the LCA. don't exit the LCA
        state = mainSource;
        while (state != LCA)
        {
            state->OnExit(this);
            state = state->GetParent();
        }

        // find the path from the LCA down to the main target state
        std::vector<State*> path;
        state = mainTarget;
        while (state != LCA)
        {
            path.push_back(state);
            state = state->GetParent();
        }

        // enter all states from the state below the LCA to the target state
        for (auto rit = path.rbegin(); rit != path.rend(); ++rit)
            (*rit)->OnEntry(this);

        // use the initial transitions to enter the leaf state 
        State *initialSource = mainTarget;
        while (initialSource->OnInitial(this))
        {
            State *initialTarget = mCurrentState;

            std::vector<State*> path;
            state = initialTarget;
            while (state != initialSource)
            {
                path.push_back(state);
                state = state->GetParent();
            }

            for (auto rit = path.rbegin(); rit != path.rend(); ++rit)
                (*rit)->OnEntry(this);
    
            initialSource = initialTarget;
        }
    }

• a ChangeState() member function that assigns the transition’s target state to the current state

As an example, the following is the code inside the OnEvent() member function of state S:

Ret S::OnEvent(HSM *context, const Event *event) const 
{
    switch (event->sig)
    {
        case Signal::I:
            if (context->mFoo)
            {
                context->mFoo = 0;
                return Ret::HANDLED;
            }
            break;

        case Signal::E:
            context->ChangeState(&HSM::s11);
            return Ret::TRANSITION;           
    }
    
    return Ret::IGNORED; 
}

The event is demultiplexed, based on its signal value, and then handled accordingly. If the event is not handled by a particular states, the event processor goes up the state hierarchy and tries to find a state which handles the event (possibly triggering a transition). If it can’t find a state that handles the event, that event gets discarded.

Code for the example is provided on GitHub

Example application: a player

As an example, I used a slightly different implementation of this hierarchical state machine in my game, as a component of my player object: the state machine takes care of the different states the player can be in (idle, moving, attacking, jumping and so on), and every frame the current state is updated. During the update the state checks the “state” (sorry, but is indeed a matter of state, no pun intended) of the player object, checking its input component, animation component, physics component and the rest. it then performs the relevant actions, or transitions to another state. The only difference with this implementation is that each state takes care of passing the buck to its superstate (using the chain of responsibility design pattern) if the event is not handled in that state, so there’s no need for returning a return code for the dispatcher. This is the result: